ここでは,チームスポーツを対象として,集団のダイナミクスに関する研究を紹介します.サッカーやホッケーなどチームスポーツは,あるルールの下で,チーム内で協調しながら,チーム間で相反する目的のために競合するという特徴を持っています.またチームのメンバーが限られていること特徴で,いわゆる集団といっても大人数ではありません.こうしたチームスポーツにおいて,二者の協調や大集団のダイナミクスと同じような何らかの規則性は見られるのでしょうか.
ホッケーのダイナミクス
チーム間の協調と競合(横山,体育学研究,認知科学)
サッカーのパスネットワーク
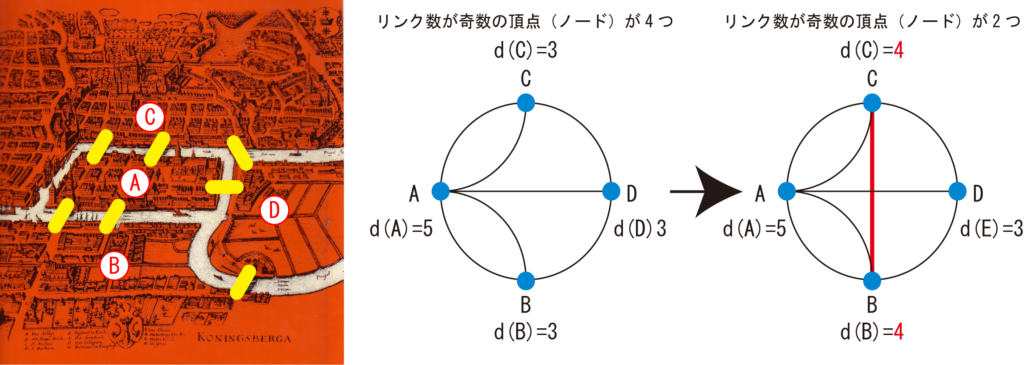
大集団のダイナミクスを明らかにするために,複雑ネットワーク理論という考え方があります.これはグラフ理論から発展してきたものです.下の図は,「ケーニヒスベルクの7つの橋の問題」と呼ばれるもので,昔,プロイセン王国(現ロシア)のケーニヒスベルクという街の4つの陸地の間に7本の橋が架かっていて,橋を一度ずつ渡り,出発した陸地に戻ってくることができるかという問題です.この問題を解いたのが有名な数学者オイラーです.彼は,陸地を頂点(vertex or node),橋を辺(edge or link)として考え,真ん中の図のような問題,いわゆる一筆書きの問題に置き換えて考えたのです.d(A)=5というのは,Aという頂点が5つの辺を持っているということで,次数(degree)と呼ばれます.そして,この次数がすべて偶数ならば一筆書きで出発点に戻れ,次数が奇数の頂点が2つで,残りが偶数であれば,奇数の頂点から出発すれば一筆書きはできるが出発点には戻れないことを明らかにしたのです.右の図では一筆書きはできますが,出発点には戻れないでしょう.
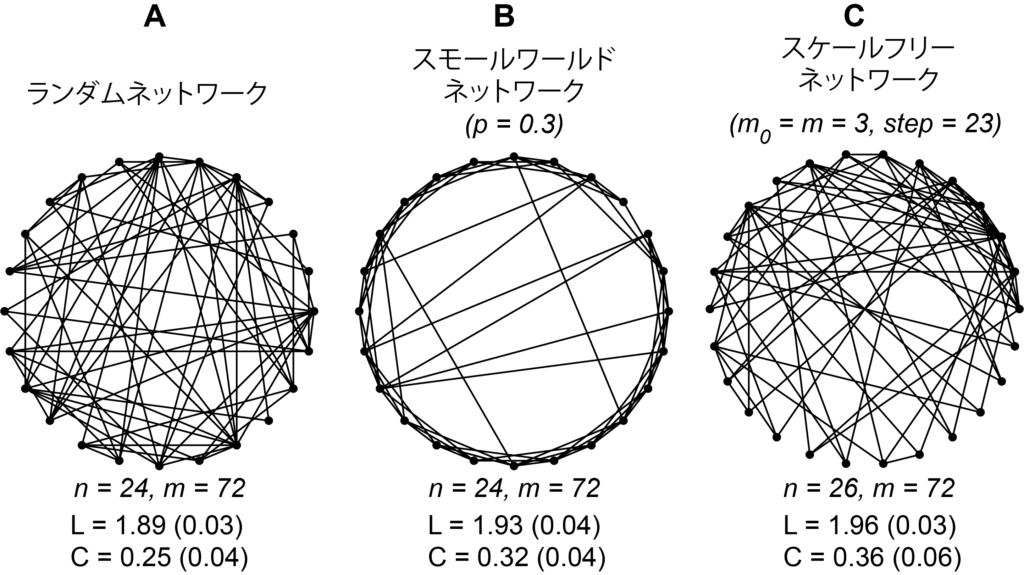
このグラフ理論をさらに発展させたのが複雑ネットワーク理論と呼ばれるもので,Erdos & Reny (1960) のランダムグラフ(図左),Watts & Strogatz (1998) の提案したスモールワールドネットワーク(図中),Barabasi & Albert (1999) のスケールフリーネットワーク(図右)が有名です.ランダムネットワークはすべての辺をランダムに繋ぎ変えたもので,スモールワールドネットワークは何本かの辺だけをつなぎ変えるとすべての頂点と少ない回数でつながるというもので,いわゆる「小さな世界」を定式化したものです.しかしながら現実のネットワーク,例えばWebページは,大きな次数を持った頂点(辺の数が多い)が数少なくあり,多くの頂点の次数は小さい(辺の数が少ない)ものです.これがスケールフリーネットワークです.このスケールフリーネットワークの特徴は,多くの辺を有するハブと呼ばれる頂点があり,その辺の数とその辺の数を有する頂点の数との関係にはベキ則が成り立つことです.現実のネットワークがスケールフリーネットワークの性質を有していることは,アメリカの電力網,俳優の共演者数などさまざまなところで実証されています.しかし,このハブの存在は,意図的な攻撃に弱いことも知られています.例えば,ハブ空港と呼ばれる大きな空港で障害がおこると,世界中の航空路線が影響を受けることからも理解できるでしょう.
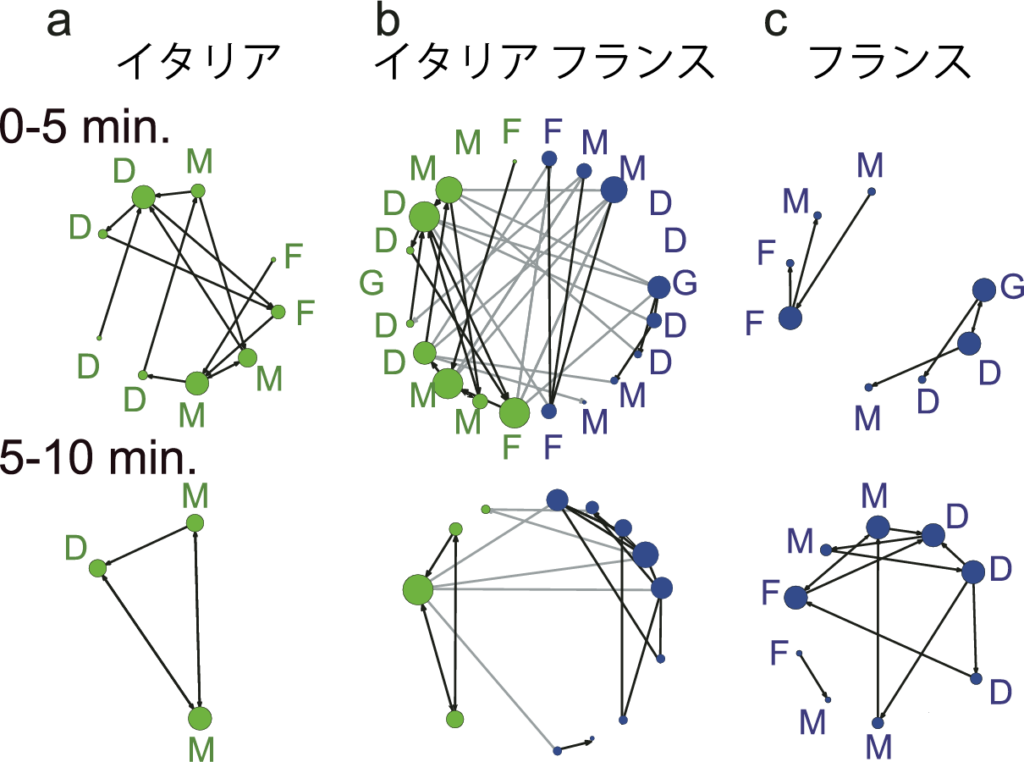
では,サッカーを題材に,試合中のパスの出し手と受け手の関係を複雑ネットワーク理論で見てみると,大規模ネットワークに共通する特徴があるのでしょうか.サッカーは11名ずつの2チームがパスを交換しながら相手ゴールを奪うゲームです.今回われわれは,2006年のワールドカップ決勝(イタリア対フランス:90分間では1対1)と2006年のキリンカップ(日本対ガーナ:0対1)のそれぞれ90分間の試合を対象として,両チーム合わせて22名の選手の間をどのようにボールが動いたかを5分間ごとに観察しました.下の図はイタリア対フランスの試合の開始5分までと5分から10分までのパスのつながりを示したものです.Fはフォワード,Mはミッドフィルダー,Dはディフェンス,Gはゴールキーパーを表しています.ただ,攻撃システムは実際の攻撃システムではなく,いわゆる4-4-2として書いてあります.
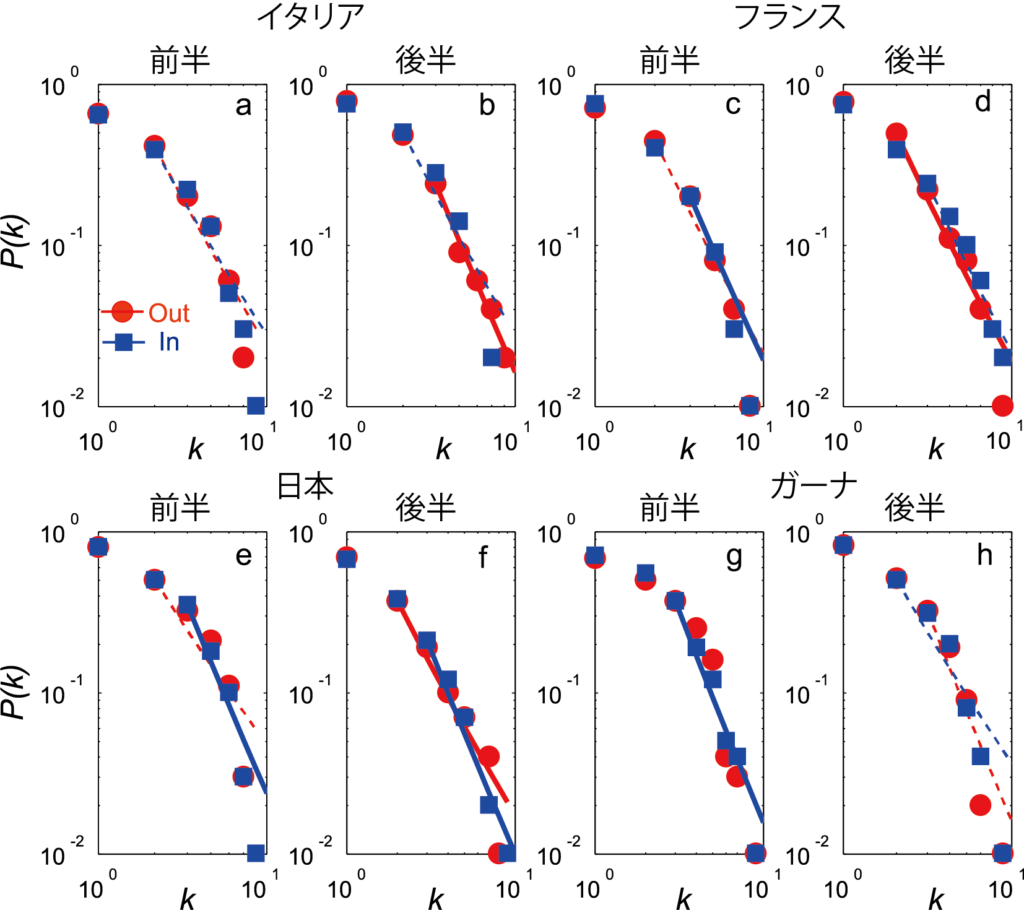
そして各選手がパスを受けた数,パスを出した数を求めた結果,多くの場合ベキ則が成り立ちました.なお,Outとあるのがパスを出した回数,Inというのがパスを受けた回数です.横軸がパスの回数,縦軸がそのパス回数の選手の確率です.横軸の左端はパス回数がゼロの選手で,その選手がたくさんいて,横軸の右側のパスを多く出したり受けたりした選手の割合は非常に小さいことがわかります.これは「司令塔」と呼ばれるパスを多く出す選手(ハブ)が存在し,逆にほとんどボールに触れない選手が多数いることを示すもので,少集団でも大集団と同様の規則性があることがわかりました.
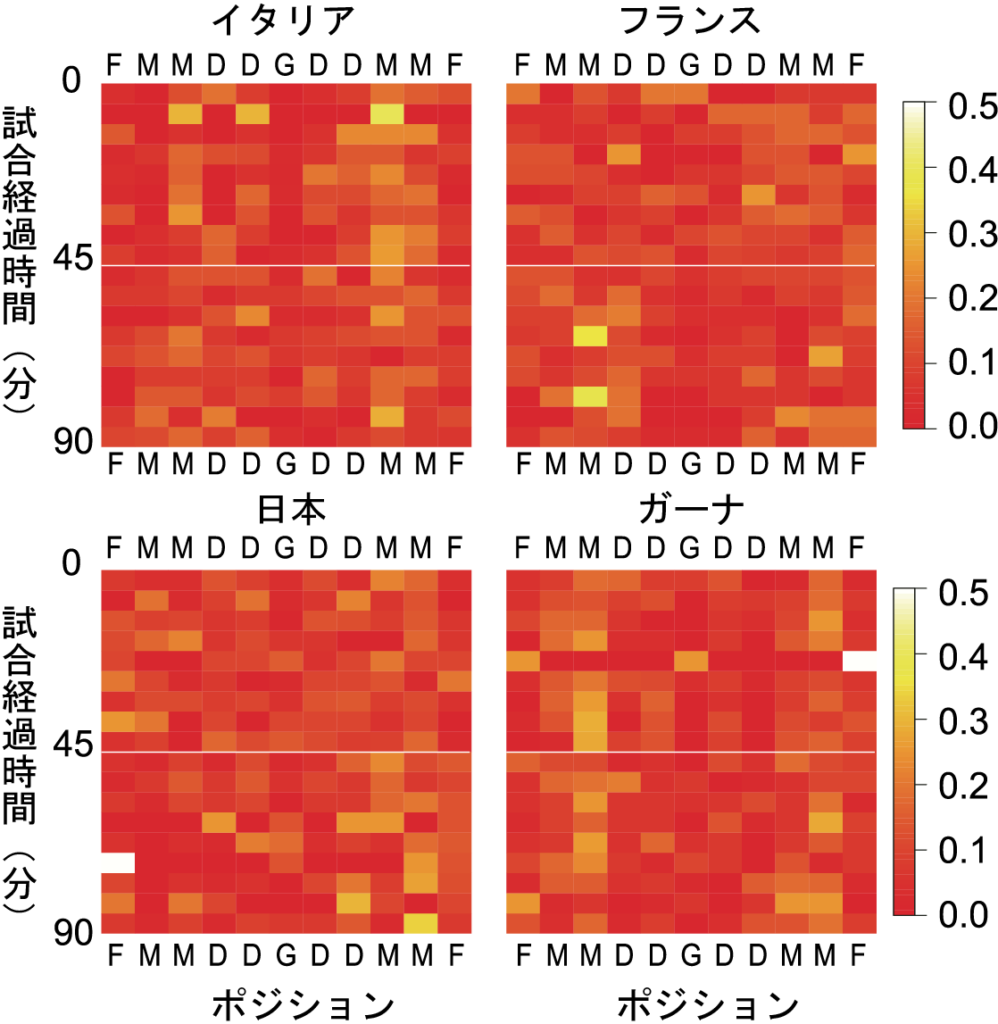
そこで,このハブとなる選手の時間変化を見ると,試合時間経過とともに変化していること(図中白っぽく見える部分が切り替わる)ことがわかりました.これは,ハブとなる選手が固定するとその選手を攻撃されて,チームとして機能しなくなるため,別の選手がハブとなり,相手からの攻撃を避けると同時にチームが機能するように,ハブとなる選手が切り替わっていると考えられます.つまり,パスのネットワークの構造を柔軟に,かつ動的に変更していると考えられ,多集団のネットワークとは明らかに異なる点です.
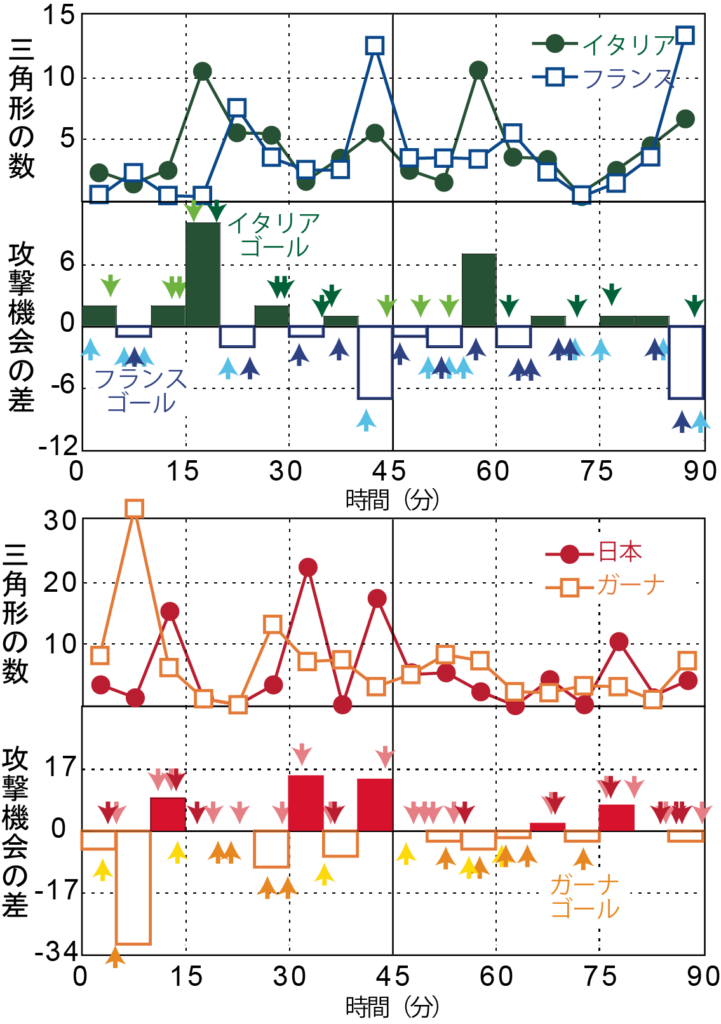
さらに,5分間ごとのパスネットワークの中で,三者の連携を示す三角形の数と,相手コート奥深くまでボールを進め,シュートチャンスを作った攻撃機会との関係を見た結果,三者間連携が多いほど,攻撃機会も多いことがわかりました.矢印が攻撃機会で濃い矢印はシュートを打ったところです.これはハブを中心に三者間連携を高めることがチームの成功に有効であることを示していると考えられます.
サッカーの試合中におけるパス回しについて,複雑ネットワーク理論から検討してみると,大規模ネットワークと共通する特徴,すなわちハブが存在することと,大規模ネットワークにはない少集団ネットワーク特有の特徴,すなわちハブが時間とともに変化するという特徴がわかりました.チームスポーツにおいても,集団のダイナミクスとしてとらえることができました.
(出典)Yuji Yamamoto & Keiko Yokoyama, Common and unique network dynamics in football games, PLoS ONE, 6, e29638, 2011.
ボールと選手の動きに潜むフラクタル
チーム内での個々の協調と,相手チームとの競合によって成り立つサッカーの攻防は,世界の多くの人を魅了します.そこには,サッカーの攻防何らかの規則性が潜み,その規則性を美しく感じ,その美しさに魅了されているのではないかと考えています.つまり,生命・自然現象に潜む普遍性のようなものがサッカーの攻防の中にもあるのではないか.このサッカーの攻防に潜む規則性を探ることを目的としたものです.
そのために,まず試合中の選手の動きを数値化する必要があります.サッカーの試合をビデオに収め,そこから選手の位置データを数値化し,さらに選手の支配領域をガウス分布で少しずつ大きくするように計算し,その試合領域を各チーム内で加算し,チーム間の間にできる境界線(前線とも呼ぶ)を求めました.その手順が以下のビデオです.
木島章文・横山慶子・門田浩二・奥村基生・鈴木啓央・山本裕二
こうやって算出したチーム間の間にできる境界線とボールの動きの時系列曲線が下の図のAとBである.サッカーコートの2つのゴール間の位置の変化を示したものである.Cは前線の位置変化の一部を切り出したものである.そしてDはCの中の一部を横を2倍,縦を3倍に拡大したものである.さらにEは,Dの一部を横2倍,縦3倍に拡大したものである.このC,D,Eの時間変化が似通っているか(相似であるか)を検討した.一般に自己相似性はすべての方向に一様に拡大・縮小されるが,このように方向によって拡大・縮小の大きさが異なる場合を,自己アフィン・フラクタルと呼ばれている.
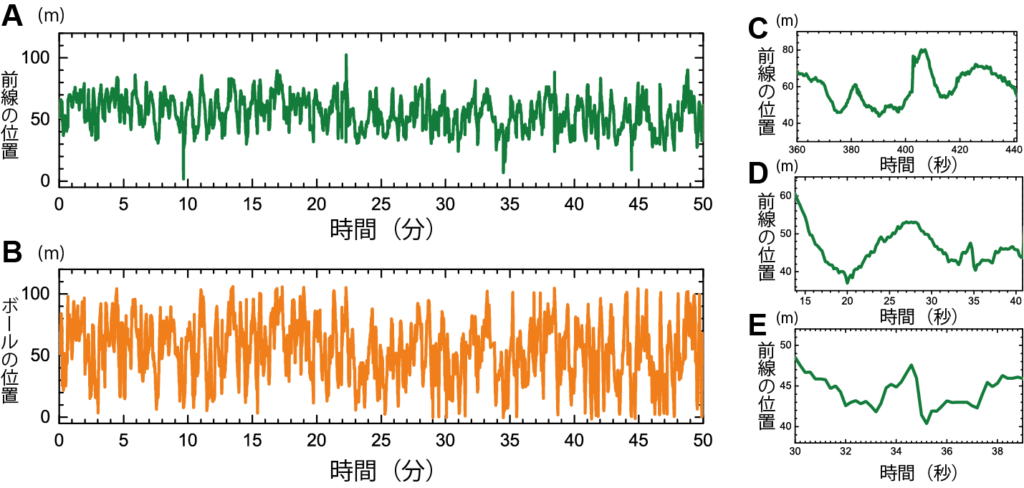
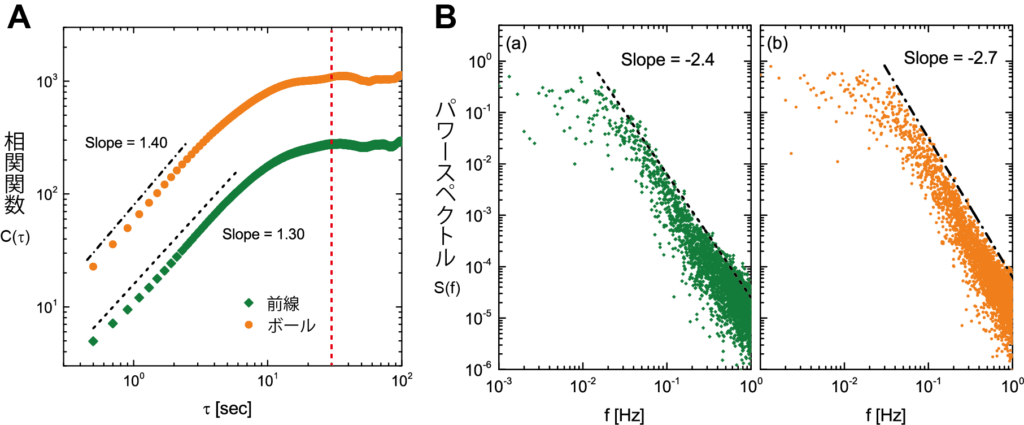
その分析結果が下の図である.Aは相関関数と呼ばれるもので,時系列の時間間隔とその間の時系列曲線の長さとの相関を求めたものである.つまり,上の時系列が自己アフィン・フラクタルであるかを検討するもので,相関関数の傾きから,自己アフィン・フラクタルを特徴づけるハースト指数 (H) を求めることができ(傾きの1/2),ここでは前線はH=0.7,ボールはH=0.65となります.このハースト指数が,1/2より大きい場合には非整数ブラウン運動といって,時系列曲線に持続性(persistence),あるいは記憶(memory)があり,H=1/2の場合にはブラウン運動,1/2より小さい場合には持続性や記憶がないとされています.つまり,ここでは30秒までの間ぐらい(赤の点線)は時間に依存した関係が見られるということです.またそれを確認するために,自己アフィンを示すベキ則のパワースペクトルを調べてみたものです.この傾きをαとすると,ハースト指数Hとの間に,α=2H+1という関係が成り立つことが知られています.今回の分析結果では,前線で-2.4,ボールで-2.7となり,ハースト指数との関係もほぼ理論通りであることが確かめられました.
これらの結果は何を意味するのでしょうか.2つのチームが相手ゴールに向かって押し合いへし合いしている様子を定量化したのが前線と呼んでいるものです.この前線やボールのゴール方向への動きは一見不規則に見えます.しかしながら,今回の結果が示唆しているのは,こうした前線やボールのある瞬間の動きがそれ以降の動きに強く影響する最長の時間(持続時間)は,プロサッカーの試合においてはおよそ30秒であるということです.逆に言うと,30秒より前の動きとはあまり関係がなく,いわゆる「ゲームの流れ」というのはないようだといえることです.つまり,直前のプレーの記憶が次の瞬間のプレーに強く影響しながらも,試合時間全体を見ると,個々の記憶は次々と忘却され,新たな記憶に上書きされ続けているといえます.この記憶と忘却の間に,ファンタジスタと呼ばれるプレーが生まれるのかもしれません.
(出典)Akifumi Kijima, Keiko Yokoyama, Hiroyuki Shima, & Yuji Yamamoto, Emergence of self-similarity in football dynamics, The European Physical Journal B, 87, 41, 2014.