力学系理論は，時間変化を記述することは前にも述べました．時間変化を記述する場合には，連続した時間変化を記述する連続力学系と，連続した時間をとびとびに離散化した離散力学系での記述が可能です．もちろん，元々離散化された時系列もあります．例えば，コインを投げ上げた時の裏表の時系列（裏，裏，表，裏・・・）などは，離散化された時系列です．離散力学系は差分方程式で書き表すことができます．以下の差分方程式は，カオスで有名なロジスティック方程式，あるいはロジスティック写像と呼ばれるものです．ここでaは定数で，以下の動画では
になっています．下がその時系列で，左上がリターンマップと呼ばれるもので，
から
への写像なので，横軸にを，縦軸にを取り，表したものです．右上は，この時系列のヒストグラムで，xの値がほぼ一様に分布しています．
$$x_{n+1} = ax_{n}(1-x_{n})$$
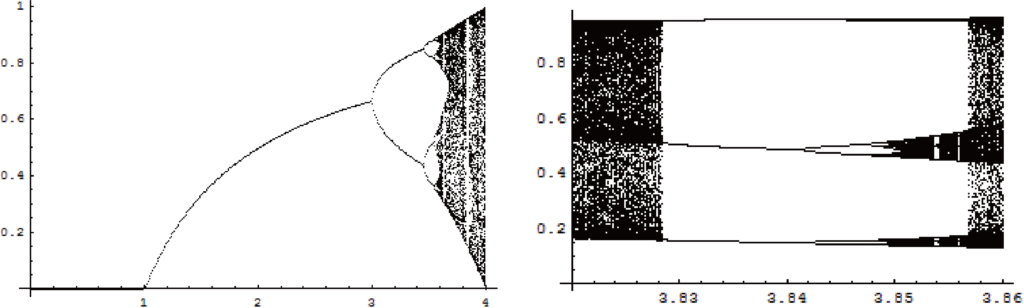
ここでaの値を変えていくと，いわゆるカオスが見られます．
の場合には，一点に収束していきますが，それ以上になると2つ（２周期），４つ（４周期）と増えていき，
になるといわゆるカオスの状態を示します．
そして，一般には連続力学系ではシステムの振る舞いは複雑に見え，そこに潜む規則性を見つけ出すのは困難になります．そこで，離散化することによって，次元を縮約し，より理解しやすくなります．この手法を見出したのは，ローレンツで，ローレンツ写像と呼ばれています．ローレンツアトラクタについては状態空間とアトラクタのところで紹介しました．この複雑に見える振る舞いの中に秩序があることを，リターンマップによって見出したのです．下の像がを見てください．ここでは
の時系列を見ていきます．そして，のピークを順番に探していきます．このピークの時系列は連続した時系列を離散可したものです．そして
と
の関係を見たのが右下のリターンマップです．3つの連立微分方程式で表されるローレンツアトラクタには，
という単純な規則（秩序）があったといえるのです．
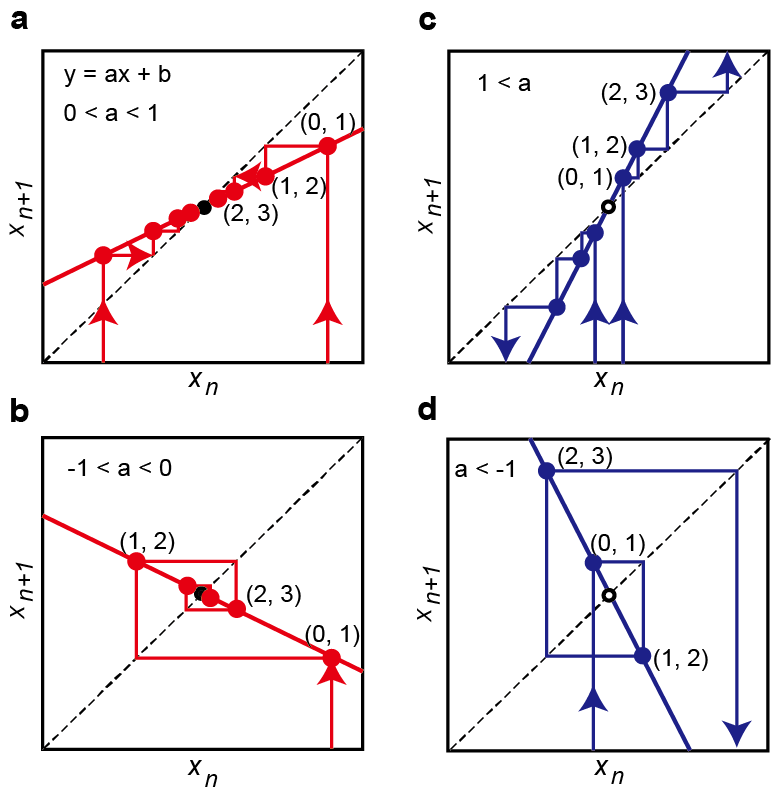
このリターンマップは，複雑に見える現象に潜む規則性を見出すためにさまざまな領域で用いられていますが，単純な関数として，
を考えると，その傾き
によって，以下の4種類のアトラクタとリペラがあることがわかります．図のaとbはアトラクタで，それぞれ漸近的に，また回転しながらアトラクタ（中心の黒い点）に近づいています．そして図のcとdは中心の白抜きの点から漸近的に，あるいは回転しながら離れていっていてリペラと呼ばれています．
